Welt ohne Gott? Entropie, Ordnung und Naturalismus

Die niedrige Entropie (respektive hohe "Ordnung") des Kosmos, die kurz nach dem Urknall vorherrschte, hat lange Zeit Rätsel aufgegeben. In dem Buch Welt ohne Gott? operiert Markus WIDENMEYER mit verschiedenen Ordnungs-Begriffen und entwickelt daraus Argumente gegen den Naturalismus der Naturwissenschaften. Seiner Meinung nach spricht die geringe Entropie des Kosmos aus Wahrscheinlichkeitsgründen gegen den Naturalismus und für einen planenden Schöpfer. Er spricht außerdem von einer mathematischen Ordnung, die allein bereits den Naturalismus "sehr unwahrscheinlich" mache. Was es damit auf sich hat, sehen wir im vorliegenden Teil unserer Besprechungsreihe.

Das Universum entstand nach Auffassung vieler Physiker in einem Zustand extrem niedriger Entropie, besaß nach WIDENMEYER also bereits zu Anfang einen hohen "Ordnungs"grad. Die Gleichsetzung von Entropie mit "Unordnung" ist, wie wir noch sehen werden, nicht besonders akkurat; genauer ist die physikalische Interpretation von Ludwig BOLTZMANN: Wenn gesagt wird, ein System, etwa ein abgeschlossener Raum, in dem sich Gasmoleküle befinden, sei in einem Zustand niedriger Entropie, ist gemeint, dass es nur wenige energetisch gleichwertige Anordnungen der Moleküle (Mikrozustände) gibt.

Im Extremfall drängen sich alle Gasmoleküle in einem sehr kleinen Teil des Raums oder ein Gasgemisch entmischt sich spontan; die Entropie wäre dann besonders niedrig. Statistisch ist die Wahrscheinlichkeit gering, dass dies passiert, weil die Gasmoleküle ungeordnet durch den Raum fliegen und ihn daher weitgehend gleichförmig ausfüllen. Ein Zustand niedriger Entropie, der mit einer lokalen Verdichtung oder Konzentrierung von Gasteilchen einhergeht, hat deshalb eine vergleichsweise geringe Wahrscheinlichkeit.

Bei gravitierenden Systemen wie dem Universum verhält es sich umgekehrt; die Gravitation sorgt für Verklumpungen, die sich zusehends verstärken. Extreme Massekonzentrationen wie Schwarze Löcher weisen daher die höchste Entropie aller bekannten Objekte im Kosmos auf: Im thermodynamischen Gleichgewicht verkörpern sie den wahrscheinlichsten Materiezustand. Umgekehrt ist eine fast völlig gleichförmige Materieverteilung, wie sie im Urknall vorkam, gleichbedeutend mit einem Minimum der Entropie.

Bis hierher lässt sich also sagen: Bestimmte Systeme mit hoher Entropie sind wahrscheinlicher als Zustände niedriger Entropie. Wenn aber eine hohe Entropie mit einem hohen Grad an Wahrscheinlichkeit einhergeht, wie erklärt sich, dass das Universum in einem Zustand extrem niedriger Entropie begann? WIDENMEYER sieht darin ein schwerwiegendes Erklärungsproblem der Naturwissenschaften:

"Der Zeitpfeil ... natürlicher, physikalischer Prozesse zeigt stets in Richtung größerer statistischer Wahrscheinlichkeit und damit größerer Unordnung des Gesamtzustands. Das gilt, wie erwähnt, für geschlossene Systeme und für das System als Ganzes. Es gilt daher auf jeden Fall für das Universum des Naturalismus. Genauso wenig können wir annehmen, dass die natürliche Ordnung schon immer vorhanden gewesen war. Es gibt hier zwei Aspekte: Wäre Ordnung schon immer vorhanden gewesen, dann müsste man eine immer größere Ordnung annehmen, je weiter man in der Zeit zurückgeht, und schließlich eine unendliche Ordnung. Dadurch wird das Erklärungsproblem aber noch gewaltiger.

Der zweite Aspekt ist, dass hier die Frage nach dem wirklichen metaphysischen Grund dieser Ordnung unbeantwortet bliebe: Wenn ein Sachverhalt wie derjenige der immensen Ordnung des Kosmos sich nicht aus sich selbst heraus verstehen lässt, wird er allein dadurch, dass man sagt, er habe schon immer existiert, keinesfalls verständlicher" (ebd., 136).

In diesem Zusammenhang kursiert immer wieder ein bestimmter Zahlenwert in den Debatten. Es handelt sich um eine Wahrscheinlichkeitsabschätzung des Physikers Roger PENROSE: Dieser hatte gezeigt, dass die fast völlig gleichförmige Anordnung der Teilchen im Raum, die kurz nach dem Urknall vorherrschte, im Vergleich zu allen übrigen Materie-Konfigurationen über alle Maßen unwahrscheinlich ist. Die Wahrscheinlichkeit, dass diese Materieanordnung und die daraus resultierende (extrem niedrige) Entropie zufällig entsteht, hat PENROSE auf 1 zu 10 hoch 10¹²³ beziffert (vgl. Luke BARNES 2012):

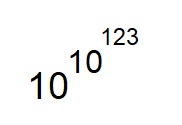
Kein Wunder, dass WIDENMEYER diese Zahl aufgreift, denn die doppelte Hochzahl ist unvorstellbar riesig. Man könnte nicht einmal die Nullen dieser Zahl aufschreiben, weil sie die Zahl aller Elementarteilchen im Universum um ein Milliardenfaches übersteigen würde:

"Wir haben eben gesehen, dass schon sehr kleine Systeme, wenn sie geordnet sind, sehr große formale Unwahrscheinlichkeiten aufweisen. Es ist daher nicht überraschend, dass unser Universum einen Ordnungsgrad besitzt, der jedes Maß an menschlicher Vorstellung weit übertrifft. Der theoretische Physiker Roger Penrose hat versucht, einen entsprechenden Grad der Ordnung des physikalischen Universums (zum Zeitpunkt eines mutmaßlichen Urknalls¹⁾) in Zahlen zu erfassen, und den Wert auf etwa 10^x mit x = 10¹²³ geschätzt, eine Zahl mit 10¹²³ Nullen." (ebd., 132)

In die Alltagssprache übersetzt bedeutet das: Die zufällige Entstehung eines weitgehend homogenen und "flachen" Raums ist unter natürlichen Bedingungen außerordentlich ungewöhnlich und unmöglich zu reproduzieren. Aus theologischer Perspektive könnte man darin ein Argument für Gott sehen, der wie ein kosmischer Uhrmacher das Universum im Zustand niedriger Entropie erschaffen habe:

"Das bisherige Ergebnis ist, dass die Ordnung des Universums nicht auf Grundlage seiner selbst erklärbar ist. Die einzige Möglichkeit scheint zu sein, dass dem System von außen Ordnung zugeführt wird. Da aber der Naturalismus das physikalische Universum als ein in sich abgeschlossenes System versteht, ist dieser Weg für ihn verbaut." (ebd., 136)

Ist der Schluss auf Gott hier also der Schluss auf die beste Erklärung? Das ist nicht der Fall.

Erstens ist die Analogie mit geordneten Systemen wie aufgeräumten Zimmern, quadratisch angeordneten Bäumen einer Baumschule (WIDENMEYER 2014, 104) usw., die den Schluss auf Planung gestatten, unbrauchbar. Derlei Beispiele beruhen auf Erfahrungswissen, sind also nur im Rahmen des Naturalismus unstrittig und plausibel. Nichts aus unserer Erfahrung spricht hingegen für einen Gott, der unendlich, immateriell, nicht zeitlich und nicht räumlich ist, der Naturgesetze hervorbringt, überschreitet usw. Die Analogie muss also mit versteckten (theologischen) Glaubensannahmen angereichert werden, damit der Schluss auf Gott plausibel erscheint. Damit ist er aber gerade kein Plausibilitätsschluss mehr.

Zudem kann ein Gott, der Naturgesetze überschreiten und Universen erschaffen kann, nie eine intellektuell zureichende Erklärung sein. Mit einer Ursache (Gott) könnte man nämlich schlicht alles "erklären": die Existenz von Universen (feinabgestimmt oder nicht), Galaxien, Sternen, Planeten, Leben, Geist, Bewusstsein usw. Das wäre eine höchst undifferenzierte Erklärung, da sich für das Wirken Gottes keine objektiven Handlungsgrenzen geschweige denn empirisch begründete Vorgehensweisen angeben lassen.

Anders gesagt: Wer "Gott" bemüht, beruft sich schlicht auf Magie, und der Verweis auf Magisches ist erkenntnistheoretisch wertlos. Ich bezeichne dies gern als die intellektuelle Todsünde des ignotum per ignotius; das bedeutet so viel wie die Rückführung von etwas Unbekanntem auf etwas noch Unbekannteres.

Zurück zur Physik: Tatsächlich gab die niedrige Entropie des Universums lange Zeit Rätsel auf, sie ist aber bereits vor Jahren von Roger PENROSE aufgeklärt worden: Anfangs besaß das Universum eine extrem niedrige Entropie, weil sich durch die enorme Ausdehnung des Raums im Urknall (kosmische Inflation) zwangsläufig alle gravitativen Verklumpungen der Materie auflösten. So war es möglich, dass sich Materie und Strahlung im frühen Universum im thermalisierten Gleichgewichtszustand befanden, wogegen sich die gravitativen Freiheitsgrade erst später durchsetzen konnten und so die Voraussetzung für die Strukturentstehung (Sterne, Planeten und Leben) schufen (Abb. 1).

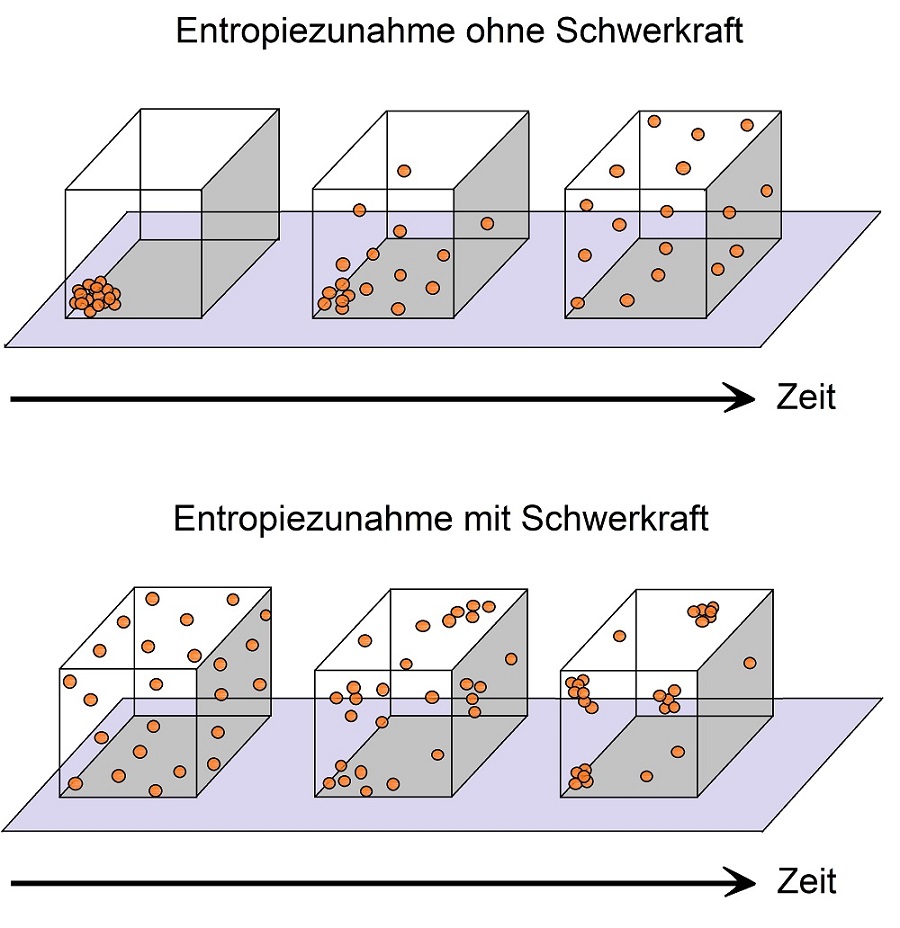
Abb.1 Der, um mit WIDENMEYER zu sprechen, Grad der "Unordnung" in einem System (Entropie) kann statistisch betrachtet im Lauf der Zeit nur zunehmen (2. Hauptsatz der Thermodynamik). Wird z.B. eine Gasflasche geöffnet, verteilen sich die Gasmoleküle gleichförmig über den gesamten Raum – das thermodynamische Gleichgewicht als Zustand maximaler Entropie wird erreicht (oben). Bei großen gravitierenden Systemen wie dem Universum führt dagegen die Schwerkraft zu lokalen Verklumpungen eines zunächst fast homogenen Gases (unten) – so sind die Sterne und Galaxien entstanden. Mit der Gravitationswirkung geht, was lange nicht bekannt war, eine Zunahme der Entropie einher. Nach PENROSE (2005, 707).

"Die Expansion des quantenmechanischen Vakuums verstärkt sich gravitativ immer weiter. Dieses exponentielle Wachstum bläht tatsächlich das Universum innerhalb der unvorstellbar kurzen Zeit von 10^–30 Sekunden um den noch weniger vorstellbaren Faktor 10⁵⁰ auf. Dies ist der lautlose Knall des Urknalls. Nach wie vor ist das Universum nicht gefeit gegen eine Energieinsolvenz … Jeden Augenblick könnte alles Bemühen wieder zu Nichts vergehen. Diesmal jedoch erwirtschaftet der Phasenübergang genügend Energie, um den Kredit zu tilgen. Den Überschuss legt das Universum an in Sachwerte: in Elementarteilchen. Die Entropie steigt mit der Entstehung dieser 10⁸⁰ Elementarteilchen drastisch an, der expandierende Raum zwischen ihnen verteilt sie jedoch nahezu homogen im Universum. Genau an dieser Stelle wird sie aufgezogen, die Uhr unseres Universums, denn diese Gleichverteilung bildet zusammen mit der Gravitationskraft jenen Zustand extrem niedriger Entropie, den wir über Jahrmilliarden allmählich erhöhen können."

Damit ist Widenmeyers Entropie-Argument gegen den Naturalismus gescheitert, denn alle relevanten Parameter wie Entropie, Enthalpie und die Energiedichte des frühen Universums resultieren aus der anfangs exponentiellen Ausdehnung von Raum und Zeit.

Richtig ist zwar, dass es für einen solchen inflationären Kosmos passende Anfangsbedingungen braucht. (Für Experten: Die Potenzialkurve des Inflaton-Feldes muss beispielsweise sehr flach sein.) Aber als Wahrscheinlichkeit für die Realisierung dieser Bedingungen kann man nicht einfach die PENROSE-Zahl hernehmen, weil dieser die unrealistische Annahme zugrunde liegt, dass die gleichförmige Materieverteilung im Urknall zufällig zustande kam.

Die Frage müsste also lauten, wie wahrscheinlich die Anfangsbedingungen für einen solchen Kosmos sind. Und es hat nicht an Versuchen gefehlt, die Wahrscheinlichkeit zu quantifizieren. Nach Ansicht des Physikers Paul STEINHARDT (2011) ist ein Universum ohne Inflation um den Faktor 10¹⁰⁰ wahrscheinlicher als eines mit Inflation. Aber solche Wahrscheinlichkeitsberechnungen kann man nicht wirklich durchführen, solange die Kosmologen nicht wissen, ob eine "gute" Inflation durch einen (bislang unbekannten) Mechanismus erzeugt wurde und ob unser Kosmos der einzige ist, der existiert. Dieses Wissen hat die Physik derzeit nicht.

Zudem ist STEINHARDTs Wahrscheinlichkeit physikalisch irrelevant, da es "vor" dem Urknall keine zeitliche Abfolge physikalischer Ereignisse gab: Quanten-Fluktuationen ändern nicht die Entropie des Vakuums, existieren also in einer fundamental zeitlosen Welt. Bildlich gesprochen stand dem Quantenvakuum die Ewigkeit zur Verfügung, um durch Fluktuationen einen inflationären Kosmos (und mit diesem Raum, Zeit und Entropie) entstehen zu lassen, der Leben ermöglich. Fluktuationen, die zu "toten" Universum führen, haben in einer Welt ohne Zeitpfeil keine physikalische bzw. wahrscheinlichkeitstheoretische Bedeutung.

Damit ist WIDENMEYERs Wahrscheinlichkeitsargument der Boden entzogen. Seinen überzogenen Anspruch gezeigt zu haben, dass mit der naturalistischen Weltsicht sehr geringe Wahrscheinlichkeiten einhergehen, oder den "Denkrahmen" des Naturalismus gar "widerlegt" zu haben (ebd., 10), kann er nicht einlösen. Er müsste nicht nur alle kosmischen Anfangs- und Randbedingungen kennen, unter denen Leben im Universum entstehen kann, er müsste auch zeigen, dass diese Bedingungen praktisch nicht realisierbar waren.

Selbst Joachim SOHNS (2015), ein der evangelikalen WORT-UND-WISSEN-Studiengemeinschaft nahestehender Physiker, hält WIDENMEYERs Entropie-Diskussion für unbrauchbar. Er bemerkt dazu auf der Internetplattform Facebook:

"Bei der Verwendung von Wahrscheinlichkeiten in der Physik und insbesondere im Zusammenhang mit der Entropie gibt es konzeptionelle Probleme und unterschiedliche Interpretationsmöglichkeiten. Die Entropie wurde ursprünglich für Systeme definiert, die aus sehr vielen gleichartigen Komponenten bestehen und sich im thermischen Gleichgewicht befinden. Ein klassisches Beispiel in Lehrbüchern ist ein Gas. Die Definition und Bedeutung der Entropie und verwandter Größen ist unter diesen Randbedingungen recht klar. Es ist aber auch unter Experten umstritten, ob und inwieweit diese Definition auf beliebige andere Systeme angewendet werden kann. Es gibt z.B. unterschiedliche Meinungen darüber, ob es sinnvoll ist, dem Universum als Ganzem eine Entropie zuzuweisen oder nicht."

Selbst wenn das Universum im Ganzen eine Entropie besitzen sollte (wovon wir einmal ausgehen), taucht diese erst mit der Entstehung von Raum und Zeit auf. Folglich kann dem ursprünglichen Quantenvakuum (dem Keim, aus dem unser Kosmos entstand) nicht unbedingt eine Entropie zugeschrieben werden. Dieses Quantenvakuum wäre bestimmten Modellen zufolge "… völlig in sich abgeschlossen und keinerlei äußeren Einflüssen unterworfen. Es wäre weder erschaffen noch zerstörbar. Es würde einfach SEIN" (HAWKING 1988, 173).

Nach Maßgabe welcher Prinzipien soll also ein naturgesetzlich strukturierter Anfangszustand (Quantenvakuum) "unwahrscheinlich" sein – könnte man das nicht mit derselben Berechtigung auch für den hochstrukturierten Geist Gottes behaupten?

Ein sich gesetzmäßig verhaltender Anfangszustand der Welt geht nicht zwangsläufig mit einer hohen Unwahrscheinlichkeit einher. SOHNS (2015), der weit davon entfernt ist, dem Naturalismus das Wort zu reden (er begrüßt sogar ausdrücklich "das Anliegen des Autors, auf die Grenzen des Naturalismus hinzuweisen"), bezeichnet WIDENMEYERs Argumentation als "verkürzend und damit irreführend".

Probleme ergeben sich auch aus dem wissenschaftlich unpräzisen, teils widersprüchlichen Ordnungsbegriff WIDENMEYERs. So wird der Begriff "Ordnung" auf alles Mögliche angewendet, beispielsweise auf:

Problematisch ist, dass sich die verschiedenen Ordnungsbegriffe teils gegenläufig verhalten: Kurz nach dem Urknall, als alle Teilchen weitgehend gleichförmig den Raum ausfüllten, gab es noch keine Strukturbildung (d. h. fast keine Ordnung-2), was für gravitative Systeme gleichbedeutend ist mit einer niedrigen Entropie (einer hohen Ordnung-3). Im hochsymmetrischen Zustand des Urknalls gab es lediglich eine Urkraft, die durch einige wenige Symmetrieprinzipien und Gesetzesaussagen beschrieben werden kann, demzufolge also nur eine geringe Ordnung-1 und Ordnung-4. Erst im Zuge fortschreitender Expansion und Abkühlung entstanden Strukturen, zu deren Beschreibung es mehr Gesetzesaussagen und Mechanismen braucht (Erhöhung von Ordnung-1 bzw. Ordnung-4).

Gravitativ bedingte Strukturbildung (Stern- und Planetenentstehung) bedingt die Zunahme von Ordnung-2, geht aber mit einer Abnahme von Ordnung-3 einher. Die Emission von Sonnenenergie wiederum verringert den Grad der Ordnung-3, ermöglicht auf der Erde aber eine komplexe Chemie (hohe Ordnung-2) sowie eine Zunahme von Ordnung-1, usw.

Welcher der vier Ordnungsbegriffe taugt nun also für den Nachweis, dass der Naturalismus "sehr Unwahrscheinliches" behauptet?

Der scheinbare Widerspruch, dass die Ordnung (je nach Definition) hoch oder niedrig sein kann, hat seinen Ursprung in der unreflektierten Gleichsetzung von Entropie mit Unordnung einerseits und "Struktur" bzw. "Naturgesetzlichkeit" mit "Ordnung" und "Unwahrscheinlichkeit" andererseits. Dieser begriffliche Wirrwarr, der keiner naturwissenschaftlichen Prüfung standhält, taugt folglich auch nicht zur Widerlegung des Naturalismus. Auch diesbezüglich zieht der evangelikale Physiker Joachim SOHNS ein erfreulich klares Resümee:

"Manche der Systeme, die Widenmeyer als Beispiele für 'Ordnung' nennt (z.B. Aufbau eines Atoms), lassen sich besser mit dem Begriff Struktur beschreiben. Es gibt Systeme, in denen ein Zustand mit Strukturen (bzw. mit höherer Ordnung) eine niedrigere Entropie aufweist. Entropie ist deshalb nicht in jedem System gleichbedeutend mit Unordnung … Befindet sich ein System weit außerhalb des thermischen Gleichgewichts und liegt auch kein lokales Gleichgewicht vor, dann ist der Makrozustand nicht eindeutig definiert. Es gibt Spezialfälle für Nicht-Gleichgewichtssysteme, in denen ein Makrozustand auf andere Weise definiert werden kann als im Gleichgewicht. Aber nicht für jedes beliebige System ist die Entropie eindeutig definiert. Widenmeyers Argumentation beansprucht Allgemeingültigkeit, diese Allgemeingültigkeit ist jedoch nicht gegeben …

Als Fazit bleibt festzuhalten, dass die Argumentation formale Fehler enthält und wichtige konzeptionelle Probleme verschwiegen werden. Gemessen an dem Anspruch, den Naturalismus zu widerlegen, ist das definitiv zu wenig."

"Genauso wenig kann man die Ordnung des Universums (oder gar das Universum überhaupt) aus der Mathematik heraus erklären. Das geht allein deshalb nicht, weil mittels der Mathematik natürlich nicht erklärt werden kann, warum das Universum überhaupt einer mathematischen Ordnung folgt. Dass das Universum einer mathematischen Ordnung folgt, macht den Naturalismus bereits sehr unwahrscheinlich. Darüber hinaus kann die Mathematik auch nicht erklären, warum es nun genau einer solchen mathematischen Ordnung folgt, wie sie für ein Universum wie das unsere nötig ist, und nicht einer von praktisch unendlich vielen anderen." (ebd., 142f)

Die Aussage, dass die Welt einer "mathematischen Ordnung folge", kann man entweder metaphorisch verstehen, dann ist sie harmlos. Oder man versteht sie im platonischen Sinn, wonach die Gesetze der Mathematik etwas real Gegebenes, mehr oder weniger Geordnetes seien und mit den Strukturen der Welt in irgendeiner Beziehung stehen. Können mathematische Terme aber überhaupt eine Ordnung haben? Welche Ordnung soll beispielsweise die folgende Gleichung besitzen?

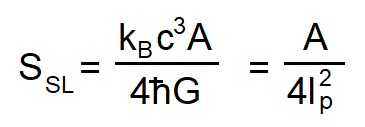
Was sagt diese Gleichung überhaupt aus? Für sich genommen rein gar nichts! Man kann diese Gleichung als Formel zur Berechnung der Oberfläche eines Schwarzen Lochs interpretieren, man kann sie aber auch als Formel zur Berechnung seiner Entropie ableiten. Oder man deutet die Formel als etwas komplett anderes, beispielsweise als dimensionslose Kennzahl oder als System-Konstante.

Gäbe es tatsächlich eine mathematische Ordnung, die in Beziehung zu den realen Verhaltensstrukturen dieser Welt steht, dann dürfte die Bedeutung einer Gleichung nicht vom Interpretationsgehalt – also von der Semantik – abhängen. Denn Ordnung ist ein ontologischer Begriff, der etwas Subjektunabhängiges beschreibt und somit von der Semantik oder der Analysenebene unabhängig ist. Das ist hier nicht der Fall.

Mit anderen Worten: Mathematische Gleichungen, Eichtheorien und Symmetrieprinzipien sind reine Beschreibungsmittel – Phantasieprodukte, wenn man so will, die man auf Teile der "geordneten" Wirklichkeit anwenden kann, aber selbst keinerlei Ordnung besitzen.

Wir sahen bereits in Teil 1 unserer Besprechungsreihe (Abschnitt 2: "Das innere Wesen der Dinge"), dass WIDENMEYER aufgrund seiner idealistischen Metaphysik bloße Abstrakta, wie etwa den Begriff der Material-Eigenschaft, den Sammel-Begriff "Materie" usw. verdinglicht (im Fachjargon nennt man diesen Kategorienfehler Reifikation). Anschließend wendet er diese idealistischen Kategorien auf den Naturalismus an, um ihn zu "widerlegen". Nach derselben Strategie verfährt er mit der Mathematik: Er fabuliert von einer mathematischen Ordnung, so als gäbe es eine Mathematik an sich, der das Universum "gehorche". Daraus folgert er, dies "mache" den Naturalismus "sehr unwahrscheinlich".

"[D]as physikalische Universum [ist] genau so eingerichtet, dass die Dinge in ihm … bestimmten mathematischen Beziehungen gehorchen, die mit Geist begabte Wesen unabhängig von der entsprechenden empirischen Forschung entdecken können. Dafür gibt es beeindruckende wissenschaftshistorische Zeugnisse. Ein Beispiel ist die Entdeckung der nicht-euklidischen Geometrie, also eines gewissermaßen gekrümmten, mathematischen Raumes durch Carl Friedrich Gauß und andere Anfang des 19. Jahrhunderts." (S.122)

Dieser Abschnitt enthält aus materialistischer Sicht mehrere ontologische Missformulierungen. Erstens: Dass das Universum eingerichtet ist, setzt den intentionalen Begriff der Einrichtung bereits voraus – ein klassischer Zirkelschluss also.

Zweitens: Die nicht-euklidische Geometrie wurde nicht entdeckt, sondern von Carl Friedrich GAUSS und Bernhard RIEMANN konstruiert. Was (später) entdeckt wurde, ist das Verhalten von Licht und anderen Dingen in der Nähe großer Massen, das mit der euklidischen Geometrie nicht mehr hinreichend genau beschreibbar war. Dann hat man ein anderes Beschreibungsmittel ausprobiert, das besser mit den Beobachtungen korrespondiert.

Aus Sicht des (gemäßigten) Konstruktivismus ist es kein Wunder, dass sich die Welt mathematisch beschreiben lässt. Bereits KANT war sich darüber im Klaren, dass wir die Welt durch die Brille unseres Wahrnehmungsapparats sehen. Wir erkennen nicht die subjektunabhängige Wirklichkeit, sondern nur das, was unser Erkenntnisapparat mit den Sinneseindrücken anstellt. Und diese Brille, die bestimmte neuronalen Aktivitätsmuster hervorbringt, gehorcht bestimmten "Bildungsregeln". Nicht verwunderlich also, dass auch unser Weltbild bestimmten, mathematischen "Bildungsregeln" folgt und nach logischen Kriterien funktioniert.

Werden die Strukturen der subjektunabhängigen Wirklichkeit nicht adäquat mithilfe der neuronalen "Logik" abgebildet, dann erleben wir beispielsweise optische Täuschungen, Halluzinationen oder Desorientierung. Warum wir nicht ständig halluzinieren und uns täuschen, liegt auf der Hand: Unsere neuronalen Erregungsmuster und das daraus generierte Weltbild müssen überlebensadäquat sein. Doch wer oder was garantiert die Überlebensadäquatheit unserer Wahrnehmungen und Erkenntnisse? Dafür braucht es keinen Gott, denn es genügt ein einfacher Selektionsmechanismus, der mithilfe der Evolutionären Erkenntnistheorie beschrieben wird – doch dazu mehr in einem späteren Teil unserer Besprechungsreihe.

Der Mathematiker David HILBERT sagt, die Mathematik sei lediglich ein formales Spiel, das bestimmten Regeln folgt. Wäre sie nicht auf die Welt anwendbar, müssten wir die Regeln des Spiels ändern oder ein anderes "Sprachspiel" erfinden. So wie die Alltagssprache und die aristotelische Logik in der Atomphysik versagt haben und neue Wege einer Quantenlogik und Metamathematik beschritten werden mussten, so deutet sich an, dass konventionelle mathematische Methoden versagen, wo die Theorie vom ganz Großen mit der Theorie des ganz Kleinen kombiniert werden muss.

Gegebenenfalls müssen zur Beschreibung quantengravitativer Prozesse abermals ganz neue mathematische oder gar metamathematische Konzepte entwickelt werden. Gut möglich auch, dass wir niemals in der Lage sein werden, bestimmte Eigenschaften der Welt bzw. des Universums mathematisch zu beschreiben. Schließlich ist unser Gehirn ein Überlebensorgan, nicht primär ein Organ des Erkennens. Aus naturalistischer Sicht ist dies verständlich: Unser Gehirn hat sich an die Gegebenheiten des Mesokosmos angepasst. Strukturen im ganz Großen und ganz Kleinen brauchen wir für das Überleben nicht zu erkennen. Deshalb wurde unser Gehirn in der Evolution nicht ausreichend "verdrahtet", um einen Quantenkosmos konsistent zu beschreiben. Es reicht völlig, wenn wir die Dimensionen, in denen sich ein Fressfeind oder Fortpflanzungspartner aufhält, adäquat beschreiben können.

Entgegen WIDENMEYER ist die Existenz einer geordneten Welt aus naturalistischer Perspektive nicht per se unwahrscheinlich. Seinen überzogenen Anspruch gezeigt zu haben, dass mit der naturalistischen Weltsicht sehr geringe Wahrscheinlichkeiten einhergehen, kann er nicht einlösen. Er müsste nicht nur alle kosmischen Anfangs- und Randbedingungen kennen, unter denen Leben im Universum entstehen kann, er müsste auch zeigen, dass diese Bedingungen praktisch nicht realisierbar waren.

Sein Entropie-Argument muss als gescheitert gelten, denn alle relevanten Parameter wie Entropie, Enthalpie und die Energiedichte des frühen Universums resultieren aus der anfangs enormen Ausdehnung von Raum und Zeit. Die daraus resultierende weitgehend gleichförmige Verteilung der Materie bildet zusammen mit der Gravitationskraft jenen Zustand extrem niedriger Entropie, der über Jahrmilliarden allmählich erhöht werden und zur Strukturbildung im Universum genutzt werden kann. Was man lange Zeit nämlich nicht wusste: Mit der Gravitationswirkung geht eine Zunahme der Entropie einher.

Davon abgesehen kann der liebe Gott aus nachvollziehbaren Gründen niemals die "beste Erklärung" für etwas sein: Der Verweis auf einen Gott ist ja nichts anderes als der Verweis auf Magie. Dies ist die intellektuelle Todsünde des ignotum per ignotius.

BARNES, L. (2012) In defence of the fine-tuning of the universe for intelligent life. Zugr. a. 24.02.2015.

GASSNER, J.M. & LESCH, H. (2014) Das aktuelle kosmologische Weltbild. In: NEUKAMM, M. (Hg.) Darwin heute: Evolution als Leitbild in den modernen Wissenschaften. WBG, Darmstadt, 51–88.

HAWKING, S.W. (1988): Eine kurze Geschichte der Zeit. Die Suche nach der Urkraft des Universums. Rowohlt, Reinbek bei Hamburg.

PENROSE, R. (2005) The road to reality. A complete guide to the laws of the universe. Vintage Books, New York.

SOHNS, J. (2015) Kommentar zu: "Zufall Notwendigkeit oder Geist? Die mathematisch-naturgesetzliche Grundordnung der Welt". Zugr. a. 30.11.2015.

STEINHARDT, P.J. (2011) Kosmische Inflation auf dem Prüfstand. Spektrum der Wissenschaft 8/11. Zugr. a. 30.11.2015.

WIDENMEYER, M. (2014) Welt ohne Gott? Eine kritische Analyse des Naturalismus. SCM Haenssler, Holzgerlingen.

[1] Nebenbei bemerkt ist die Formulierung "mutmaßlicher Urknall" entlarvend, weil sie dafür spricht, dass WIDENMEYER die Urknalltheorie ablehnt. Dass es einen Urknall gab, ist empirisch aber so gut belegt wie die Annahme, dass die Erde Kugelgestalt hat – unabhängig davon, ob man den Kosmos als eines übernatürlichen Anstoßes bedürftig wähnt. Dies legt wiederum nahe, dass WIDENMEYER ein unnötiges Vorhutgefecht betreibt, denn in Wahrheit scheint ihm daran gelegen zu sein, die evangelikale Bibelinterpretation salonfähig zu machen, die nicht nur die Faktizität der Evolution, sondern auch des Urknalls leugnet. Damit überreizt er aber seinen Ansatz: Selbst, wenn alle Argumente des Autors folgerichtig und beweiskräftig wären (was sie nicht sind), wäre bestenfalls der Deismus von Gottfried Wilhelm LEIBNIZ gestützt, wonach Gott macht, dass sich die Dinge von allein entwickeln (evolvieren).

Entropie, Ordnung und die "Widerlegung" des Naturalismus

Besprechung des Buches "Welt ohne Gott" - Teil 4